Exploratory data analysis

class: center, middle, inverse, title-slide

.title[
# Exploratory data analysis
]
.author[
### Sara Mortara & Andrea Sánchez-Tapia
]
.institute[
### re.green | ¡liibre!
]
.date[
### 2022-07-13
]

---

## today

- exploratory data analysis

- descriptive statistics

- exploratory graphics

- variable relationships

---

## Explanatory Data Analysis - John Tukey

.pull-left[
<img src="figs/tukey.jpg" width="300" style="display: block; margin: auto;" />
]

.pull-right[
<img src="figs/John_Tukey.jpg" width="293" style="display: block; margin: auto;" />
]

---
## get to know your data!

---
## goals of EDA

1. control data quality
--

2. suggest hypotheses for observed patterns
--

3. support the choice of statistical procedures for hypothesis testing
--

4. assess whether the data meet the assumptions of the chosen statistical procedures
--

5. indicate new studies and hypotheses

---

## alert!

EDA does not mean

it is assumed that the researcher has formulated *a priori*  __hypotheses__  supported by __theory__

---
## tips

- there is no recipe!
--

- can take between 20-50% of analysis time
--

- can be started during data collection
--

- visual techniques are widely used
--

---

## the importance of graphics and the Anscombe quartet

- created by mathematician Francis Ascombe
--

- 4 datasets with the same descriptive statistics but very different graphically

---

## Anscombe data

.tiny[

```r
# the dataset already exists inside R
data("anscombe")
```

```r
# mean
apply(anscombe, 2, var)
```

```
##        x1        x2        x3        x4        y1        y2        y3        y4 
## 11.000000 11.000000 11.000000 11.000000  4.127269  4.127629  4.122620  4.123249
```

```r
# variance
apply(anscombe, 2, var)
```

```
##        x1        x2        x3        x4        y1        y2        y3        y4 
## 11.000000 11.000000 11.000000 11.000000  4.127269  4.127629  4.122620  4.123249
```
]

---
## let's take a look into the data

```
##    x1 x2 x3 x4    y1   y2    y3    y4
## 1  10 10 10  8  8.04 9.14  7.46  6.58
## 2   8  8  8  8  6.95 8.14  6.77  5.76
## 3  13 13 13  8  7.58 8.74 12.74  7.71
## 4   9  9  9  8  8.81 8.77  7.11  8.84
## 5  11 11 11  8  8.33 9.26  7.81  8.47
## 6  14 14 14  8  9.96 8.10  8.84  7.04
## 7   6  6  6  8  7.24 6.13  6.08  5.25
## 8   4  4  4 19  4.26 3.10  5.39 12.50
## 9  12 12 12  8 10.84 9.13  8.15  5.56
## 10  7  7  7  8  4.82 7.26  6.42  7.91
## 11  5  5  5  8  5.68 4.74  5.73  6.89
```

---
## correltion between x and y

.tiny[

```r
# correlation
cor(anscombe$x1, anscombe$y1)
```

```
## [1] 0.8164205
```

```r
cor(anscombe$x2, anscombe$y2)
```

```
## [1] 0.8162365
```

```r
cor(anscombe$x3, anscombe$y3)
```

```
## [1] 0.8162867
```

```r
cor(anscombe$x4, anscombe$y4)
```

```
## [1] 0.8165214
```

]

---
## coefficients of the linear model

.tiny[

```r
# correlation
coef(lm(anscombe$x1 ~ anscombe$y1))
```

```
## (Intercept) anscombe$y1 
##  -0.9975311   1.3328426
```

```r
coef(lm(anscombe$x2 ~ anscombe$y2))
```

```
## (Intercept) anscombe$y2 
##  -0.9948419   1.3324841
```

```r
coef(lm(anscombe$x3 ~ anscombe$y3))
```

```
## (Intercept) anscombe$y3 
##   -1.000315    1.333375
```

```r
coef(lm(anscombe$x4 ~ anscombe$y4))
```

```
## (Intercept) anscombe$y4 
##   -1.003640    1.333657
```

]

---
## now let's actually look into the Anscombe data

---
## guiding questions

1. Where is the data centered? How is the data distributed? Are the data symmetrical, asymmetrical, bimodal?
--

2. Are there outliers?
--

3. Do the variables follow a normal distribution?
--

4. Are there relationships between the variables? Are the relationships between variables linear?
--

5. Do variables need to be transformed?
--

6. Was the sampling effort the same for each observation or variable?

---
class: inverse,  middle, center

# descriptive statistics

---
## questions to ask the data

1. are there are missing values i.e. (__NA__s)? Are they really missing?
 
2. area there many __zeroes__?

3. where is the data centered? how are they spread? are they symmetrical? skewed, bimodal?

4. are there extreme values (outliers)?

5. what is the distribution of the variable?

---
## descriptive statistics

| Parameter | Description | R function |
|------|-------------|--------|
| average | arithmetic mean | mean() |
| median | core value | median() |
| mode | most frequent value | sort(table(), decreasing = TRUE)[1] |
| standard deviation | variation around the mean | sd() |
| quantiles | cut points dividing a probability distribution | quantile() |

---
class: inverse,  middle, center

# exploratory graphics

---

## reading data in R

```r
# reading data generated in the last class
all_data <- read.csv("data/processed/03_Pavoine_full_table.csv")
# reading environmental data
envir <- read.csv("data/raw/cestes/envir.csv")
# environmental data without site
envir.vars <- envir[, -1]
```

---

## visualizing data in a boxplot

```r
boxplot(all_data$Abundance)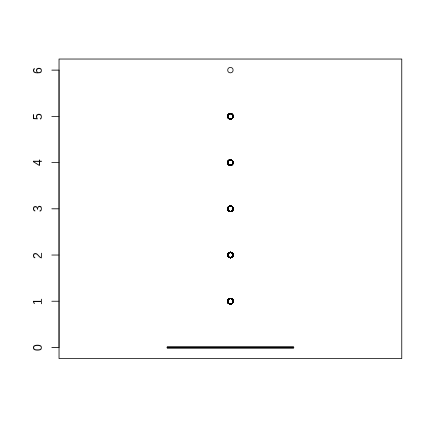
```

---

## going back to the data

```r
summary(all_data$Abundance)
```

```
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##  0.0000  0.0000  0.0000  0.1788  0.0000  6.0000
```

```r
# how many zeroes
sum(all_data$Abundance == 0)
```

```
## [1] 4824
```

```r
# what proportion?
sum(all_data$Abundance == 0)/nrow(all_data)
```

```
## [1] 0.8880707
```

---

## understanding the boxplot

---

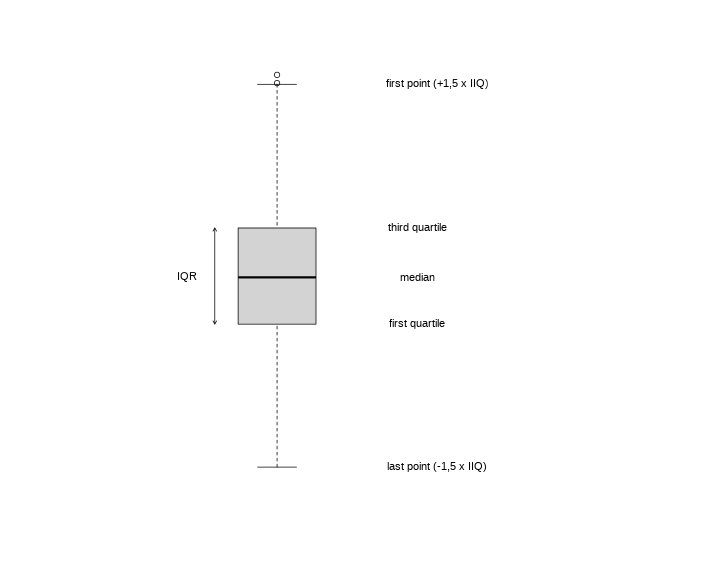
## visualizing data in a histogram

```r
hist(all_data$Abundance)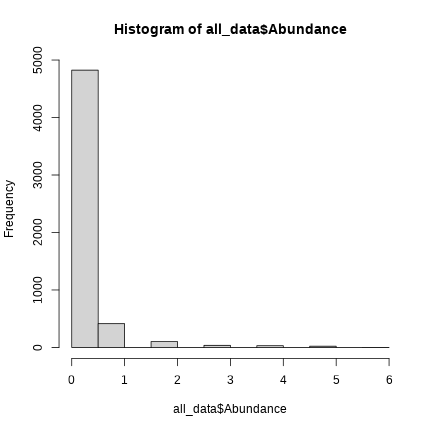
```

---

## types of histogram

.tiny[

```r
par(mfrow = c(1,2))
hist(all_data$Abundance)
hist(all_data$Abundance, probability = TRUE)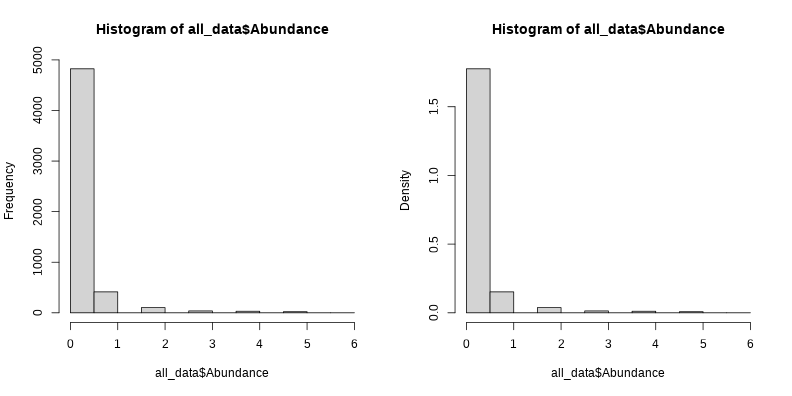
```

```r
par(mfrow = c(1,1))
```

]

---
## classes of histogram

.tiny[

```r
par(mfrow = c(1,3))
hist(all_data$Abundance, 
     breaks = seq(0, max(all_data$Abundance), length = 3))
hist(all_data$Abundance,  
     breaks = seq(0, max(all_data$Abundance), length = 5))
hist(all_data$Abundance)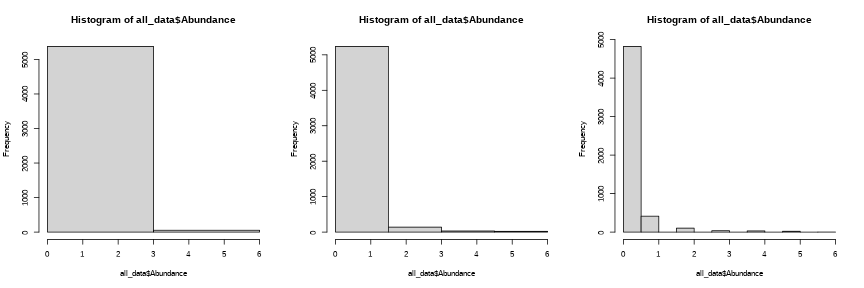
```

```r
par(mfrow = c(1,1))
```

]

---

## empirical probability density curves

represents the function that describes the probability of finding a certain value

```r
hist(all_data$Abundance, probability = TRUE )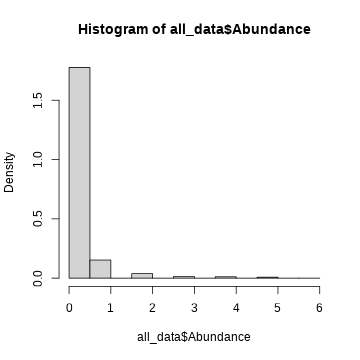
```

---

## empirical probability density curves

```r
plot(density(all_data$Abundance))
```

---

## does the distribution fit the data?

discrete and asymmetric distribution --> Poisson?

```r
# maximum of abundance
ab.max <- max(all_data$Abundance)
# lambda
ab.med <- mean(all_data$Abundance)
```

---
## does the  __Poisson__ distribution fit the data?

```r
hist(all_data$Abundance, probability = TRUE)
points(dpois(0:ab.max, ab.med), col = cor[5])
lines(dpois(0:ab.max, ab.med), col = cor[5])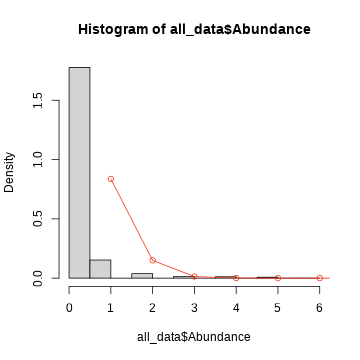
```

---
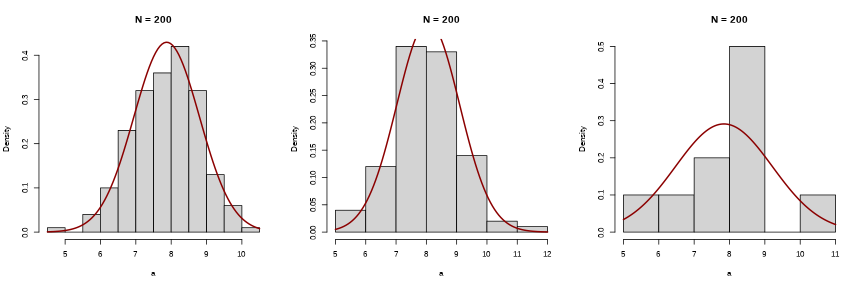
## statistical distributions: Gaussian or normal

---
## why is sampling important?

---
class: inverse, middle, center

# relationships between variables

---

## scatter plot

```r
plot(Clay ~ Silt, data = envir.vars, pch = 19)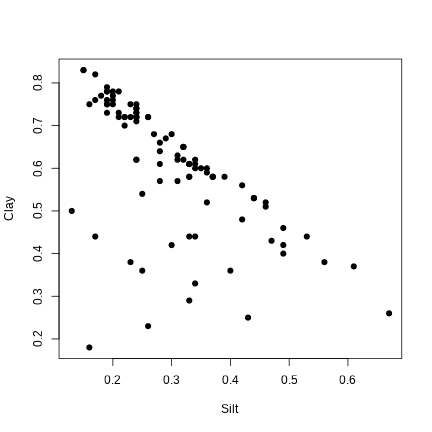
```

---

## correlation between variables

.tiny[

```r
cor(envir.vars)
```

```
##              Clay        Silt        Sand        K2O          Mg      Na100g
## Clay    1.0000000 -0.62694838 -0.71786978  0.4422121  0.18895961  0.28623195
## Silt   -0.6269484  1.00000000 -0.07660720 -0.2388823 -0.02370373  0.02738666
## Sand   -0.7178698 -0.07660720  1.00000000 -0.3364384 -0.21930954 -0.37588031
## K2O     0.4422121 -0.23888226 -0.33643842  1.0000000  0.33549979  0.25314016
## Mg      0.1889596 -0.02370373 -0.21930954  0.3354998  1.00000000  0.41377118
## Na100g  0.2862320  0.02738666 -0.37588031  0.2531402  0.41377118  1.00000000
## K       0.5436153 -0.32123692 -0.40584268  0.5681411  0.41177702  0.57075510
## Elev   -0.1485992  0.08087163  0.09379561 -0.1767765 -0.22314328 -0.33392061
##                 K        Elev
## Clay    0.5436153 -0.14859923
## Silt   -0.3212369  0.08087163
## Sand   -0.4058427  0.09379561
## K2O     0.5681411 -0.17677652
## Mg      0.4117770 -0.22314328
## Na100g  0.5707551 -0.33392061
## K       1.0000000 -0.33251202
## Elev   -0.3325120  1.00000000
```

]

---
## correlation between variables

[By DenisBoigelot](https://commons.wikimedia.org/w/index.php?curid=15165296)

---

## correlation between variables

.tiny[

```r
pairs(envir.vars)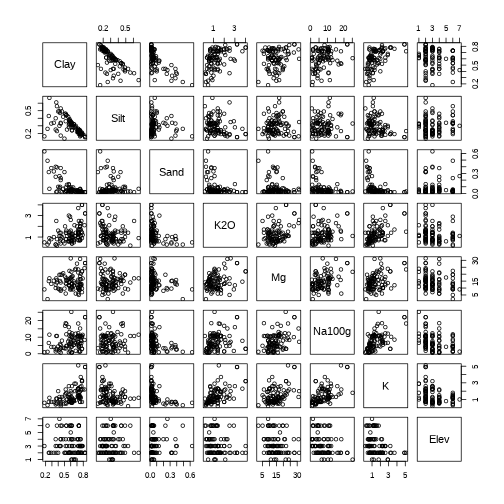
```

]

---
## even better visualization

---
class: center, middle

# and what are the paths for the data analysis?

your __[ H Y P O T H E S I S ]__

---

## after the __[ H Y P O T H E S I S ]__, what are the paths?

1. understand the data well
--

2. variable response is normal? --> __lm__ and other parametric analysis
--

3. variable response has another distribution -->  non-parametric analysis, __glm__
--

4. hierarchical predictor variables? --> __(g)lmm__
--

5. pseudo-replication in space or time -->  __(g)lmm__
--

---
## todo

- create and run script `04_eda.R`

- `git add`, `commit`, and `push` of the day

---
class: center, middle

# ¡Thanks!

<center>
<svg viewBox="0 0 512 512" style="position:relative;display:inline-block;top:.1em;fill:#A70000;height:1em;" xmlns="http://www.w3.org/2000/svg">  <path d="M476 3.2L12.5 270.6c-18.1 10.4-15.8 35.6 2.2 43.2L121 358.4l287.3-253.2c5.5-4.9 13.3 2.6 8.6 8.3L176 407v80.5c0 23.6 28.5 32.9 42.5 15.8L282 426l124.6 52.2c14.2 6 30.4-2.9 33-18.2l72-432C515 7.8 493.3-6.8 476 3.2z"></path></svg> [saramortara@gmail.com](mailto:saramortara@gmail.com) | [andreasancheztapia@gmail.com](mailto:andreasancheztapia@gmail.com)