Statistical modeling

class: center, middle, inverse, title-slide

.title[
# Statistical modeling
]
.author[
### Sara Mortara & Andrea Sánchez-Tapia
]
.institute[
### re.green | ¡liibre!
]
.date[
### 2022-07-19
]

---

## about

1. concepts in statistical modeling

2. probability distributions

3. the linear model

---
class: center, middle, inverse
# 1. concepts in statistical modellng

---
class: center, middle, inverse

# connect theory with data using statistical models

---
## best references

.pull-left[
<img src="figs/ecological_detective.jpg" width="300" style="display: block; margin: auto;" />

]

.pull-left[
<img src="figs/burnham_anderson.jpeg" width="300" style="display: block; margin: auto;" />

]

---
## best references

.pull-left[
<img src="figs/ben_bolker.jpg" width="300" style="display: block; margin: auto;" />

]

.pull-left[
<img src="figs/ecological_statistics.jpg" width="300" style="display: block; margin: auto;" />

]

---
## model & data

- data are not sacrossanct
- search for a minimal and suitable model

---

## the data

- continuous or dicrete variable?
- how many replicates?
- what are the predictor variables?
- what is the pattern?

## concepts

- maximum likelihood
- principle of parsimony 
  - Ocram's razor 
  
---
## maximum likelihood

given the data and the model:

what are the parameter values that make the data more plausible?

---
## principle of parsimony

.pull-left[

> all things
being equal, the
simpler solution
is the
best

William of Occam
]

.pull-right[
<img src="figs/occams_razor.jpg" width="851" />

]

---
## principle of parsimony

- models with fewer possible parameters
- linear models preferable to non-linear
- less assumptions
- minimally adequate models
- simpler explanations

---
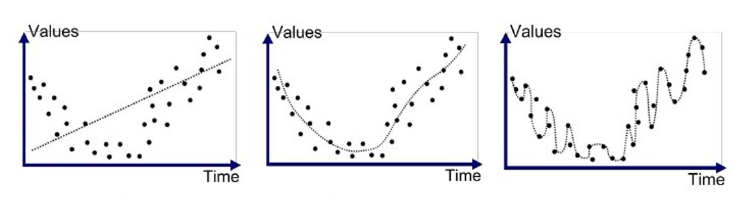
## best model is just a model

- all models are wrong <img src="figs/melting_face.png" width="41" />
- some models are better than others
- we are never sure of the correct model
- the simpler the model, the better -- but not simplistic

---
class: center, middle, invert
# 2. statistical distributions

---
## statistical distributions

.tiny[

distribution  | type | `$E(X)$` | `$\sigma^2(X)$` | usage | example
------------- | -----| -------|-----------|----------|-------------
normal | continuous | `$\mu$` | `$\sigma^2$` | Symmetric curve for continuous data | size distribution
binomial | discrete | `$np$` | `$np(1-p)$` | Number of successes in `$n$` attempts | Presence or absence of species
Poisson | discrete | `$\lambda$` | `$\lambda$` | Independent rare events where `$\lambda$` is the rate at which the event occurs in space or time | Distribution of rare species in space
Log-normal | continuous | `$log(\mu)$` | `$log(\sigma^2)$` | Asymmetric curve | Species abundance distribution

]

---
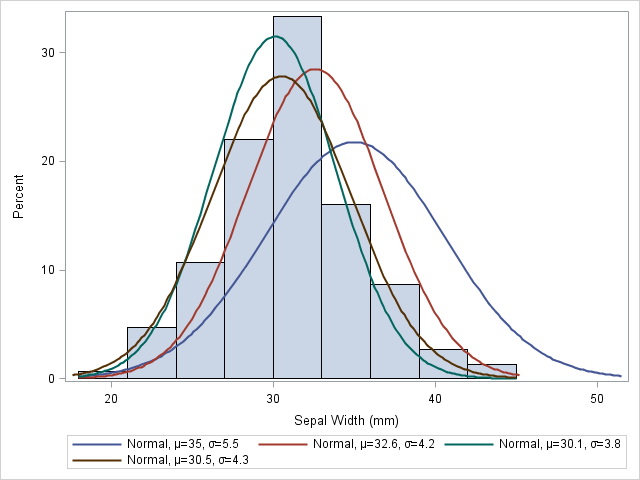
## continuous distributions

```r
df_n <- data.frame(val = rnorm(1000, mean = 0, sd = 1))
df_ln <- data.frame(val = exp(rnorm(1000)))
```

---
## continuous distributions

.pull-left[

<img src="07_slides_files/figure-html/unnamed-chunk-11-1.png" style="display: block; margin: auto;" />
]

.pull-right[

]

---
class: center, middle, inverse
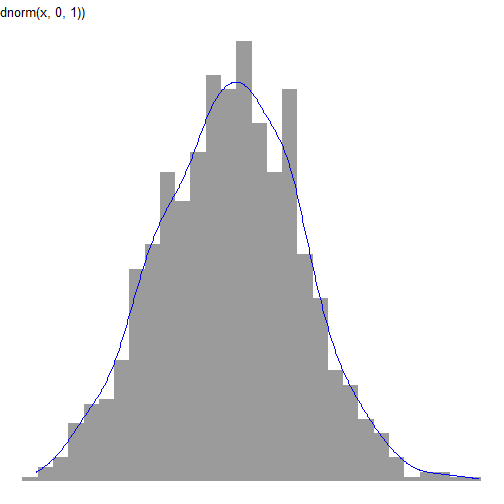
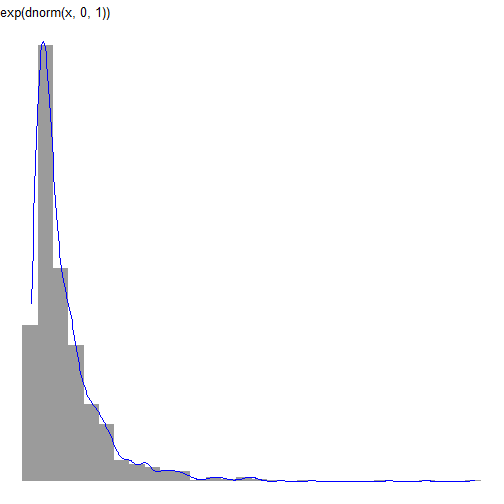
# 3. the linear model

mathematical model + uncertainty: `$Y  = a + bx + \epsilon$`

---
## statistical model

---
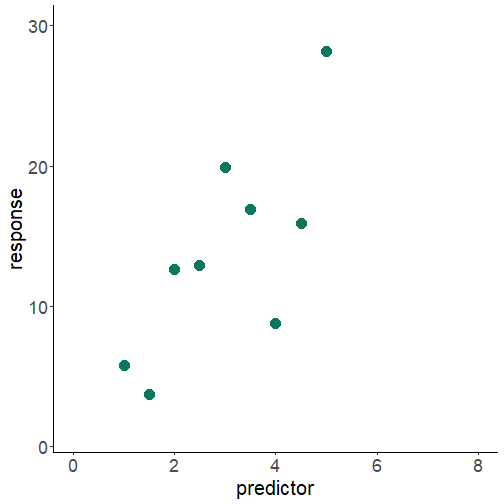
## relation between variables: prediction

---
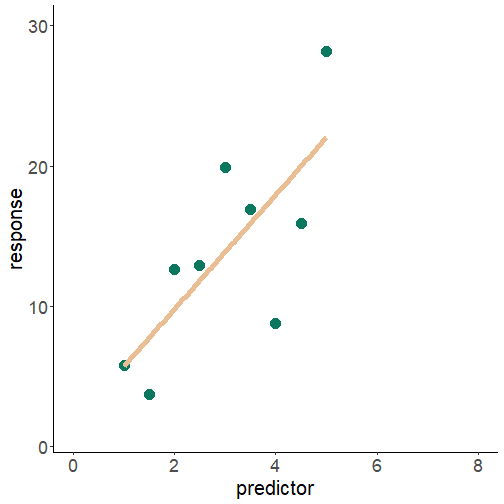
## relation between variables: extrapolation

---

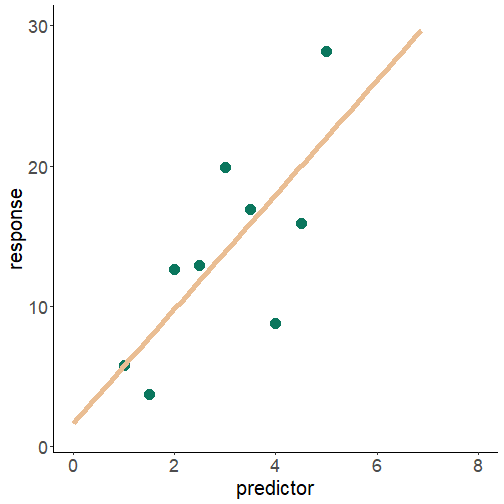
## the linear model

.pull-left[
`$$y = a + bx$$`

`$$y = \alpha + \beta X + \epsilon$$`

`$$\epsilon = N (0, \sigma)$$`

]

.pull-right[

<img src="07_slides_files/figure-html/unnamed-chunk-15-1.png" style="display: block; margin: auto;" />
]

---
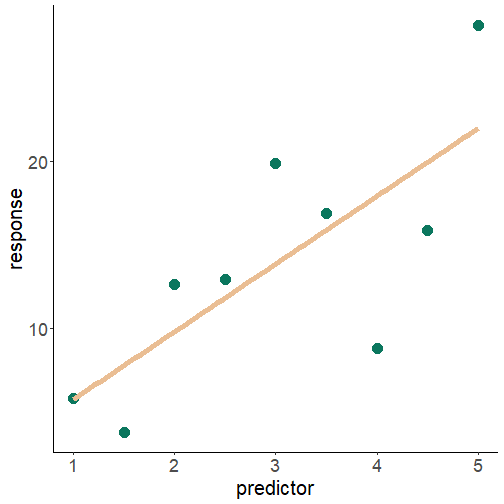
## is the response variable normal?

---
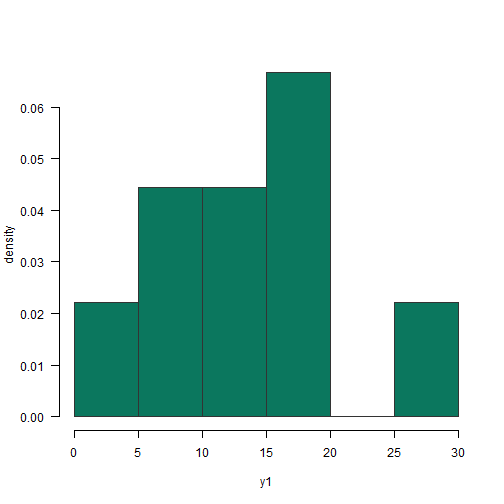
## is the response variable normal?

---

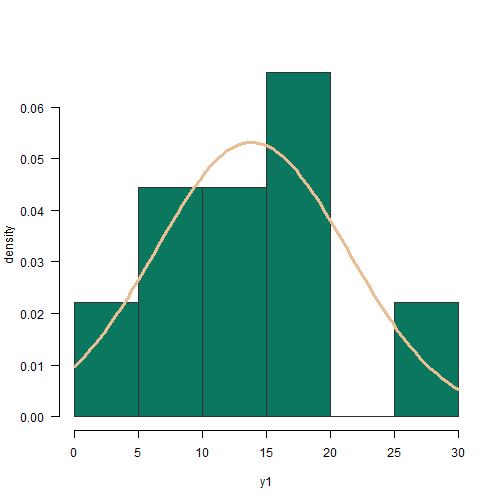
## what is relationship between the predictor and the response variable?

---
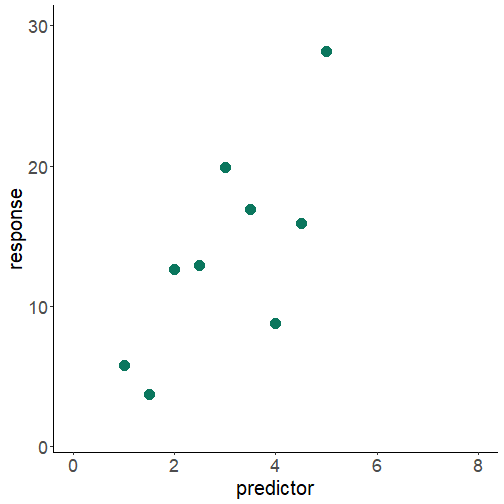
## assumptions

+ relationship between x and y is linear

+ normality of residuals

+ __homoscedasticity__ -- homogeneity of residuals variance

+ independence of residuals error terms

---

## parameter estimation

.pull-left[
- least squares method
- maximum likelihood

]

.pull-right[
![](figs/noun-parameters-4125642.svg)
]
---
## least squares method

---
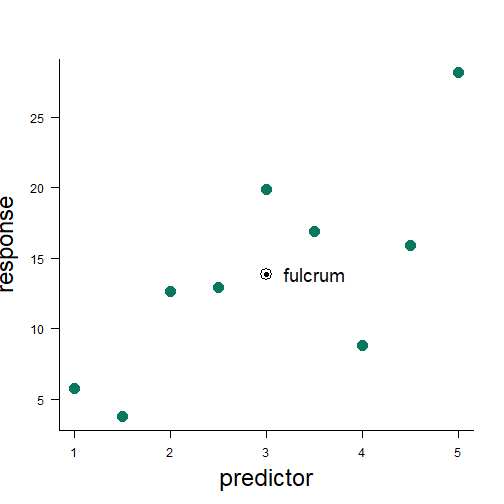
## least squares method

---
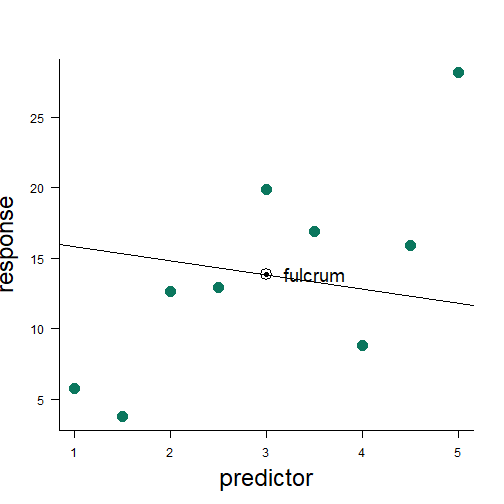
## least squares method

---
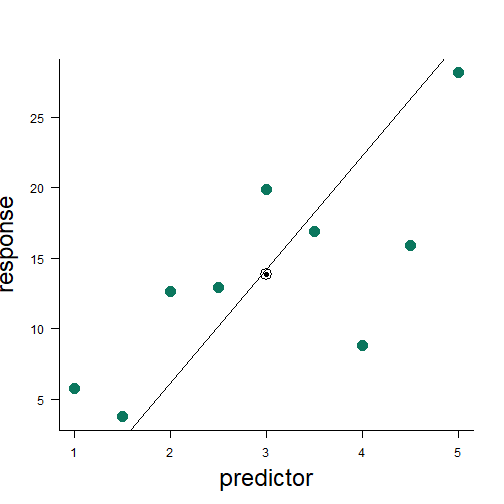
## least squares method

---

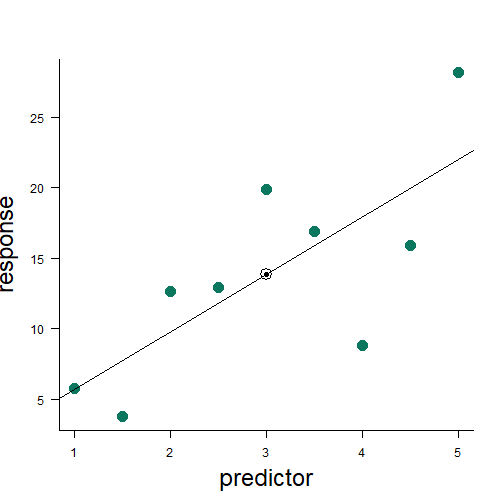
## linear model in R

.tiny[

```r
mod <- lm(y1 ~ x1)
summary(mod)
```

```
## 
## Call:
## lm(formula = y1 ~ x1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -9.1424 -4.0088  0.9982  2.8714  6.1706 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)  
## (Intercept)    1.632      4.520   0.361   0.7287  
## x1             4.076      1.384   2.945   0.0216 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 5.361 on 7 degrees of freedom
## Multiple R-squared:  0.5534,	Adjusted R-squared:  0.4895 
## F-statistic: 8.672 on 1 and 7 DF,  p-value: 0.02156
```

]

---
## uncertainty in the estimate

.tiny[

`$$y = 1.63 + 4.08x + \epsilon$$`

]

estimation of coefficients

.tiny[

```r
coef(mod)
```

```
## (Intercept)          x1 
##    1.632390    4.075949
```
]

confidence interval

.tiny[

```r
confint(mod)
```

```
##                  2.5 %    97.5 %
## (Intercept) -9.0566136 12.321394
## x1           0.8031237  7.348775
```
]

---
## linear model residue

---
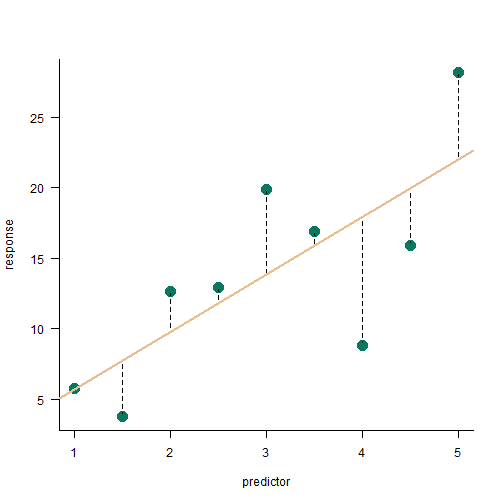
## linear model variance partitioning

sum of squares from the linear model

`$$SS_{total} = SS_{between} + SS_{error}$$`

---

## total sum of squares

.pull-left[
`$$SS_{total} = \sum_{i=1}^n (y_{i} - \bar{y})^2$$`
]

.pull-right[
<img src="07_slides_files/figure-html/unnamed-chunk-25-1.png" style="display: block; margin: auto;" />
]

---
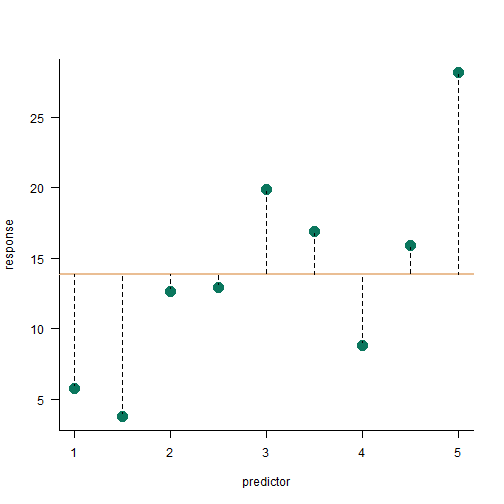
## total sum of squares

`$$SS_{total} = \sum_{i=1}^n (y_{i} - \bar{y})^2$$`

`$$SS_{total} = 450.35$$`

---
## residual sum of squares

.pull-left[

`$$SS_{error} = \sum_{i=1}^n (y_{i} - \hat{y}_i)^2$$`

]

.pull-right[
<img src="07_slides_files/figure-html/unnamed-chunk-27-1.png" style="display: block; margin: auto;" />
]

---
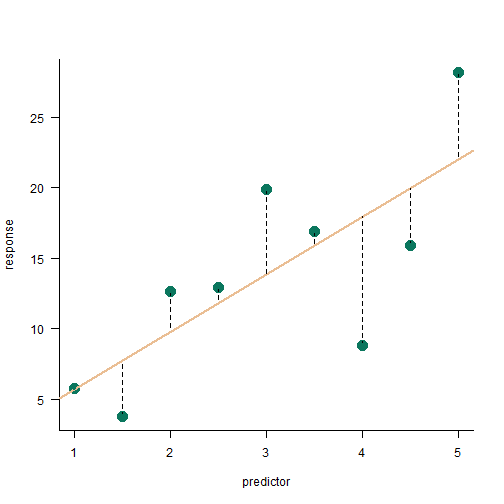
## residual sum of squares

`$$SS_{error} = \sum_{i=1}^n (y_{i} - \hat{y}_i)^2$$`

`$$SS_{error} = 201.15$$`

---
## model sum of squares

`$$SS_{total} = SS_{between} + SS_{error}$$`

`$$SS_{between} = SS_{total} - SS_{error}$$`

`$$SS_{between} = 450.35 - 201.15$$`

`$$SS_{between} = 249.2$$`

---
## variance partitioning

`$$SS_{total} = 450.35$$`

`$$SS_{between} = 249.2$$`

`$$SS_{error} = 201.15$$`

---
## variance partitioning

__anova table__

.tiny[

```r
anova(mod)
```

```
## Analysis of Variance Table
## 
## Response: y1
##           Df Sum Sq Mean Sq F value  Pr(>F)  
## x1         1 249.20 249.200  8.6723 0.02156 *
## Residuals  7 201.15  28.735                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
```

]

---
## coefficient of determination `$R^{2}$`

`$$R^2 = \frac{SS_{between}}{SS_total}$$`

`$$R^2 = \frac{249.2}{450.35}$$`

`$$R^2 = 0.5533$$`

---
## coefficient of determination `$R^{2}$`

.tiny[

```r
summary(mod)
```

]

---
## todo

- `lm` tutorial

- `git add`, `commit`, and `push` of the day

---
class: center, middle

# ¡Thanks!

<center>
<svg viewBox="0 0 512 512" style="position:relative;display:inline-block;top:.1em;fill:#A70000;height:1em;" xmlns="http://www.w3.org/2000/svg">  <path d="M476 3.2L12.5 270.6c-18.1 10.4-15.8 35.6 2.2 43.2L121 358.4l287.3-253.2c5.5-4.9 13.3 2.6 8.6 8.3L176 407v80.5c0 23.6 28.5 32.9 42.5 15.8L282 426l124.6 52.2c14.2 6 30.4-2.9 33-18.2l72-432C515 7.8 493.3-6.8 476 3.2z"></path></svg> [saramortara@gmail.com](mailto:saramortara@gmail.com) | [andreasancheztapia@gmail.com](mailto:andreasancheztapia@gmail.com)